ГЕОМЕТРІЯ

Урок №13-14 (09.03)

Многогранники. Призма, її елементи. Пряма і правильна призми. Перерізи призми.

Призма — це многогранник, дві грані якого є рівними многокутниками,

що знаходяться в паралельних площинах, а інші грані — паралелограми.

Основи призми – це грані, які знаходяться в паралельних площинах,

а інші грані — бічні грані призми.

Залежно від основи призми бувають:

— трикутними,

— чотирикутними

— шестикутними та ін.

Призма з бічними ребрами, перпендикулярними її основам, називається прямою призмою.

Пряма призма називається правильною, якщо її основи — правильні многокутники.

Висота призми - це відстань між основами призми .

Призма, бічні ребра якої не перпендикулярні основам, називається похилою призмою.

Зверніть увагу! Висота прямої призми збігається з боковим ребром.

Висота похилої призми — це перпендикуляр, проведений між основами призми. Часто перпендикуляр проводять з однієї з вершин верхньої основи.

Переріз призми площиною, яка проходить через два бічні ребра, які не належать одній грані, називається діагональним перерізом призми

Домашнє завдання:

Написати конспект, вивчити визначення а також виконати наступні завдання:

1. Побудуйте переріз куба ABCDA₁B₁C₁D₁ площиною, що проходить через точки K, P, T — середини ребер A₁B₁, BB₁ і B₁C₁ (сторінка 43 підручника) https://lib.imzo.gov.ua/wa-data/public/site/books2/pidruchnyky-11-klas-2019/13-matematyka-11-klas/matematyka-11-kl-bevz.pdf

2. На бічних ребрах AA₁, BB₁ і CC₁ прямокутного паралелепіпеда ABCDA₁B₁C₁D₁дано точки M, N і P відповідно. Побудуйте переріз паралелепіпеда площиною, що проходить через точки M, N і P. (сторінка 43-44 підручника) https://lib.imzo.gov.ua/wa-data/public/site/books2/pidruchnyky-11-klas-2019/13-matematyka-11-klas/matematyka-11-kl-bevz.pdf

Виконайте тестове завдання https://naurok.com.ua/test/join?gamecode=9930041

Надіслати викладачу лише фото виконаних завдань

Урок №15-16 (16.03)

Площі бічної і повної поверхонь призми.

Перегляньте відео https://www.youtube.com/watch?v=wDLL5V3p5WI

Розв'яжіть задачі

1.Всі ребра трикутної призми дорівнюють по 3дм.Чому дорівнює площа бічної поверхні призми?

2. Основа прямої трикутної призми – прямокутний трикутник з катетами 3 см і 4 см. Висота призми 10 см. Чому дорівнює площа повної поверхні призми?

Урок №17-18 (23.03)

Паралелепіпед. Прямокутний паралелепіпед. Властивості паралелепіпеда.

Паралелепіпедом називається призма, основи якої є паралелограмами.

Усі грані прямокутного паралелепіпеда – прямокутники.

Довжини трьох ребер прямокутного паралелепіпеда, які виходять з однієї вершини, називаються лінійними розмірами (або вимірами) прямокутного паралелепіпеда. Паралелепіпед називається прямим, якщо в нього бічні ребра перпендикулярні до основ.

Властивості паралелепіпеда

Протилежні грані паралелепіпеда попарно рівні та паралельні.
Усі діагоналі паралелепіпеда перетинаються в одній точці та діляться нею навпіл

Прямий паралелепіпед має всі властивості паралелепіпеда, і, крім того, бічні грані прямого паралелепіпеда є прямокутниками.

Прямий паралелепіпед, основами якого є прямокутники, називається прямокутним.

Властивості прямокутного паралелепіпеда

Усі діагоналі рівні.
Квадрат діагоналі дорівнює сумі квадратів трьох його вимірів.

Прямокутний паралелепіпед, у якого всі ребра рівні, називається кубом.

Перегляньте відео https://www.youtube.com/watch?v=04xbG49Ytwc

Виконайте тестове завдання https://naurok.com.ua/test/join?gamecode=8056703

Урок №19-20 (30.03)

Розв'язування задач. Тест-контроль.

«Теорія без практики мертва І безплідна, практика без теорії не можлива»

Дослухаємося до цих слів і пригадаємо теорію.

Письмово дайте відповіді на наступні запитання:

1. Як називається многогранник, який складається з двох плоских многокутників, що лежать в різних площинах і суміщаються паралельним перенесенням, і відрізків, які з’єднують відповідні точки цих многокутників?

2. Як називаються сторони граней многогранника?
У якій призмі бічні ребра перпендикулярні до основи?

3. Як знайти площу бічної поверхні прямої призми?

4. Паралелепіпедом називається призма, в основі якої лежить ..?

5. Яка фігура є бічною гранню призми?

6. Як називається точка в якій сходяться три грані куба?

7. Що у прямої призми може бути висотою?

8. Як знайти повну поверхню призми?

9. Довжини непаралельних ребер прямокутного паралелепіпеда називаються…Світ, що нас оточує – це світ геометрії. Сьогодні на уроці ми повторимо основні властивості многогранників та формули обчислення їх поверхонь та будемо роз’язувати задачі з даної теми.

Задача 1. Основою прямої призми є прямокутний трикутник з гіпотенузою 10 см і катетом 6 см. Знайти площу бічної поверхні призми, якщо її бічне ребро дорівнює 5 см.

Площу бічної поверхні прямої призми обчислюємо за формулою:
Sб=P•H,
де P – периметр основи;
H – висота прямої призми, довжина бічного ребра.
У прямокутному трикутнику ABC (∠BAC=90), в якому AB=6 см – катет і BC=10 см – гіпотенуза, за теоремою Піфагора знайдемо катет BC – третю сторону основи прямої призми:
AC2=BC2-AB2, звідси

Обчислимо периметр основи прямої призми:
P=AB+BC+AC=6+8+10=24 см.
Обчислимо площу бічної поверхні прямої призми з бічним ребром H=CC1=5 см:
Sб=P•H =24•5=120 см2.

Відповідь: 120 см2.

Задача 2. Сторона основи правильної трикутної призми дорівнює 12 см, а діагональ бічної грані дорівнює 13 см. Знайти бічну поверхню призми.

Бічну поверхню правильної призми обчислюємо за формулою:
Sб=Soc•H,
де Soc – площа основи;
H – висота правильної призми, довжина бічного ребра.
У правильному трикутнику ABC (AB=BC=AC=a=12 см) периметр обчислимо за формулою Poc=3a=3•12=36 см.
Оскільки кожна бічна грань правильної призми є прямокутник, то бічне ребро перпендикулярне до площини основи, тоді BB1⊥BC, а B1C=13 см – діагональ грані BB1C1C.
У прямокутному трикутнику B1BC (∠B1BC=90), в якому BC=12 см – катет і B1C=13 см – гіпотенуза. За теоремою Піфагора знайдемо катет BB1=H – висоту, довжину бічного ребра правильної призми:

BB12=B1C2-BC2, звідси

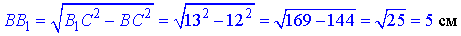
Обчислимо площу бічної поверхні правильної трикутної призми:
Sб=Soc•H=36•5=180 см2.

Відповідь:180 см2.