Ознака паралельності прямих. Розв’язування задач.
ГЕОМЕТРІЯ
Тема : Паралельність прямих і площин у просторі.
Тема уроку: Ознака паралельності прямих. Розв’язування задач.
Однією з основних фігур у просторі, як і на площині, є пряма. Ви вже знаєте, як можуть розташовуватися прямі на площині. З'ясуємо, яким може бути розташування двох прямих у просторі.
Означення. Дві
прямі в просторі називаються паралельними, якщо вони лежать
в одній площині і не перетинаються.
Через дві паралельні прямі завжди можна
побудувати єдину площину.
Отже, у просторі, як і
на площині, прямі можуть перетинатися або бути паралельними, тоді вони лежать в
одній площині.
Відшукайте на каркасній моделі прямокутного
паралелепіпеда прямі,
які не перетинаються і не лежать в одній площині?

(Такі прямі є – це прямі АВ і D1D, прямі BC і A1A….
Вони
паралельні?(Ні, оскільки не лежать в одній площині.)
Ці прямі називаються мимобіжними.
Як би ви сформулювали означення мимобіжних
прямих?
Означення. Дві
прямі простору, які не перетинаються і не лежать в одній площині,
називаються мимобіжними.
Ознака паралельності прямих
Теорема. Якщо дві прямі паралельні третій, то вони паралельні між собою.
Доведення цієї теореми нескладне, тому пропоную розібрати її доведення за підручником.
Ознака мимобіжності прямих
Теорема. Якщо одна пряма лежить у деякій площині, а друга —перетинає цю площину в точці, що не належить першій прямій, то такі дві прямі — мимобіжні.
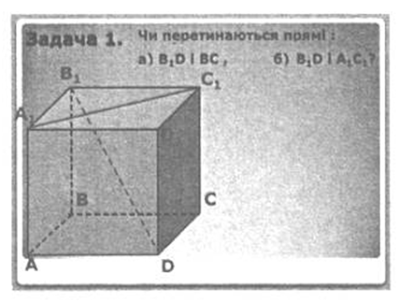
Розв'язування задач за готовими рисунками
Пряма B1D перетинає площину (АВС) у точці D, яка не належить
прямій ВС.
Отже, прямі В1D і ВС – мимобіжні (за ознакою
мимобіжності прямих), а тому B1D і ВС не
перетинаються.
Розв’язання
Пряма MD перетинає площину (АВС) у точці D, яка не
належить прямій АС.
Отже, прямі MD i AC – мимобіжні (за
ознакою мимобіжності прямих), а тому MD i AC не перетинаються.
Розв’язання
EF – середня лінія трикутника ADC, отже
EF||AC. MN – середня лінія трикутника АВС, тому MN||AC.
Отже, EF||MN за ознакою паралельності прямих.
Сьогодні ми розібралися з дуже важливим питанням — розташуванням прямих у просторі. Усі просторові геометричні фігури, з якими ви познайомитеся пізніше, можна побудувати за допомогою прямих. Знання властивостей, якими вони пов'язані, дають змогу розв'язати багато важливих задач, серед яких більшість прикладного характеру.