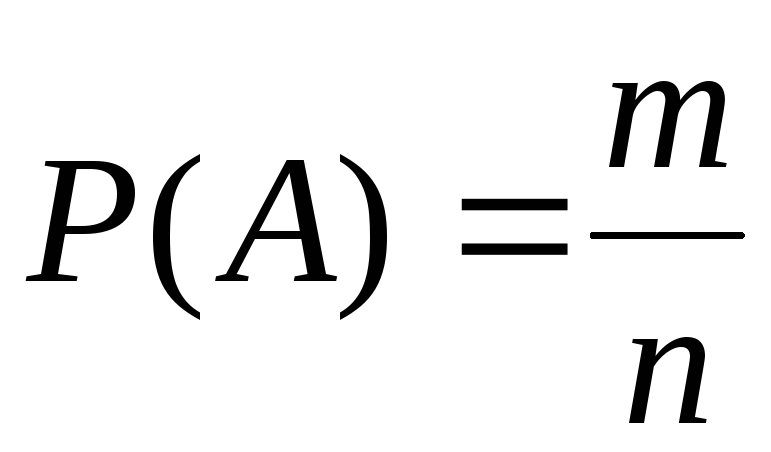Основні поняття теорії ймовірностей.Операції над подіями. Ймовірність суми несумісних подій.

АЛГЕБРА
Тема 3: Початки теорії ймовірностей

Урок 21-22 Основні поняття теорії ймовірностей. Операції над подіями. Ймовірність суми несумісних подій.  
http://zno.academia.in.ua/mod/book/view.php?id=3242
https://web.posibnyky.vntu.edu.ua/fitki/4tichinska_teoriya_jmovirnostej/1.htm
Класичне означення ймовірності

Для кількісного вимірювання появи випадкових подій і їх комбінацій вводиться поняття ймовірності події, що є числом такої ж природи, як відстань у геометрії або маса в теоретичній механіці.
Імовірністю випадкової події А називається невід'ємне число Р(А) що дорівнює відношенню числа елементарних подій які сприяють появі А до кількості всіх елементарних подій простору :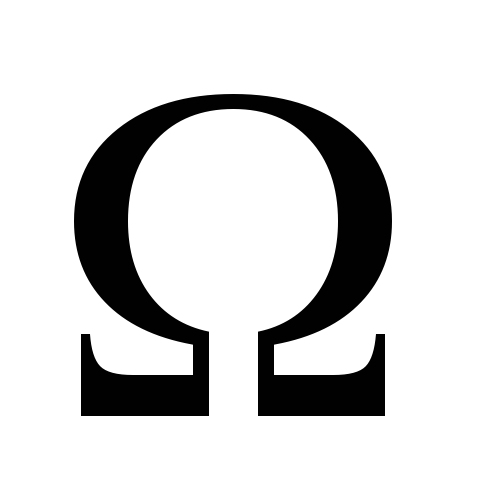


Для неможливої події 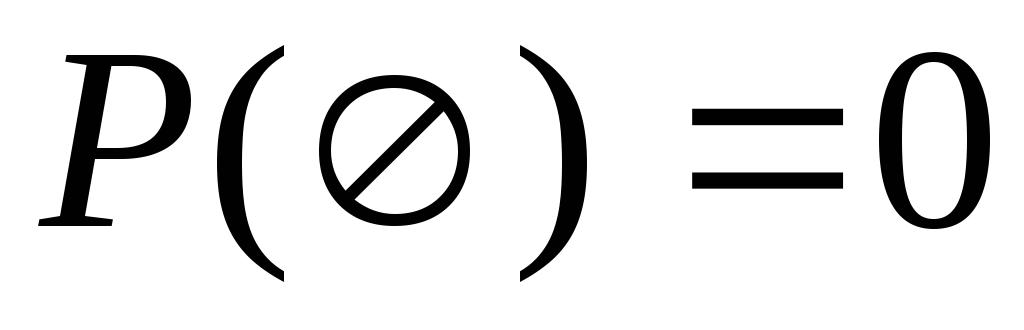(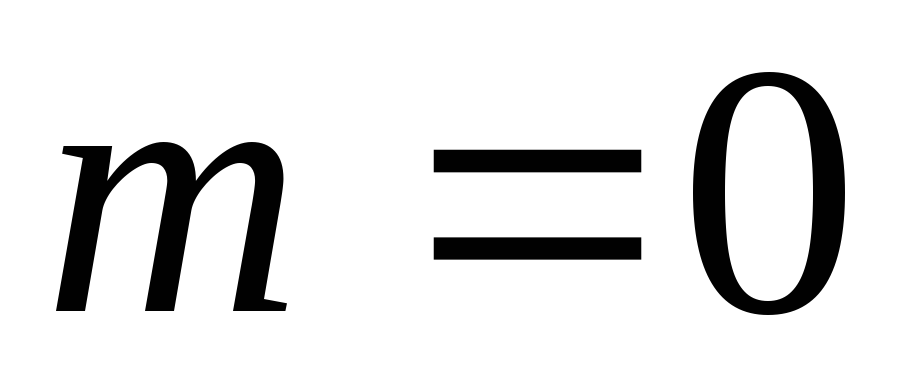). Для вірогідної події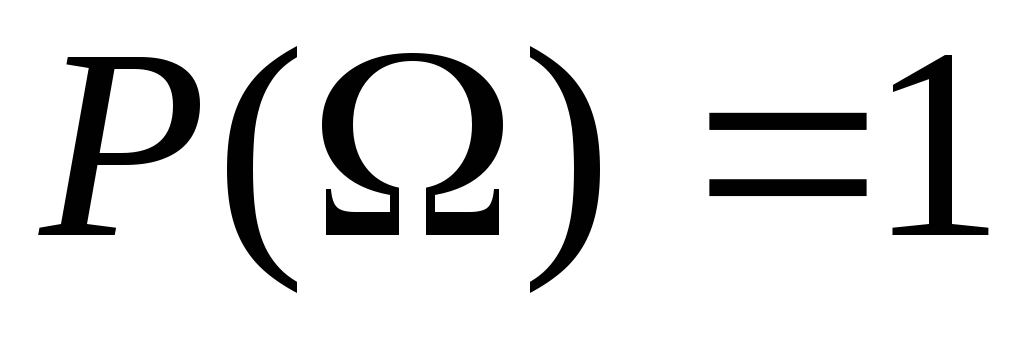. Отже, для довільної випадкової події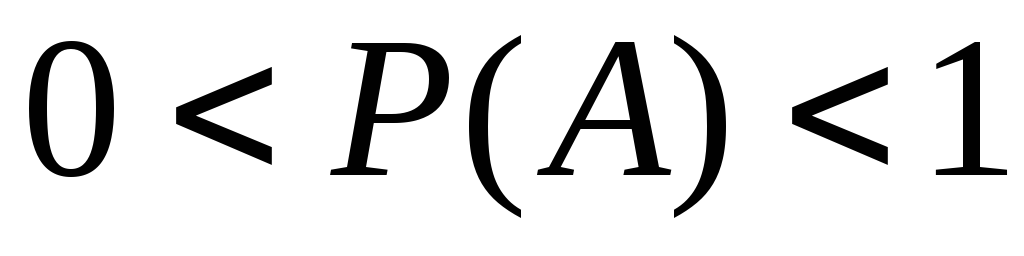(оскільки 0 <m < n).

Приклад. У ящику міститься 15 однотипних деталей, із яких 6 бракованих, а решта — стандартні. Навмання з ящика береться одна деталь. Яка ймовірність того, що вона буде стандартною?
                                                              Розв'язання. 
Число всіх рівноможливих елементарних подій для цього експерименту: 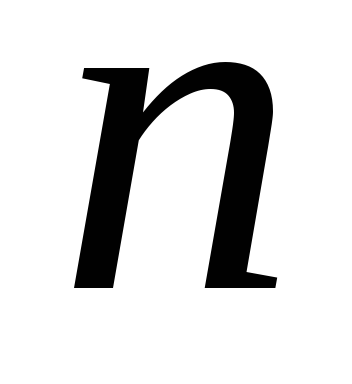=15.
Нехай А — подія, що полягає в появі стандартної деталі. Число елементарних подій, що сприяють появі випадкової події А, дорівнює дев'яти (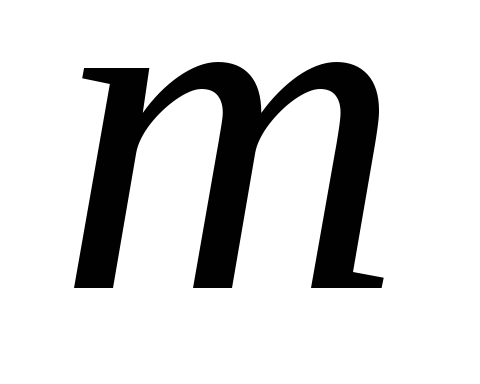= 9). Згідно з формулою маємо:.

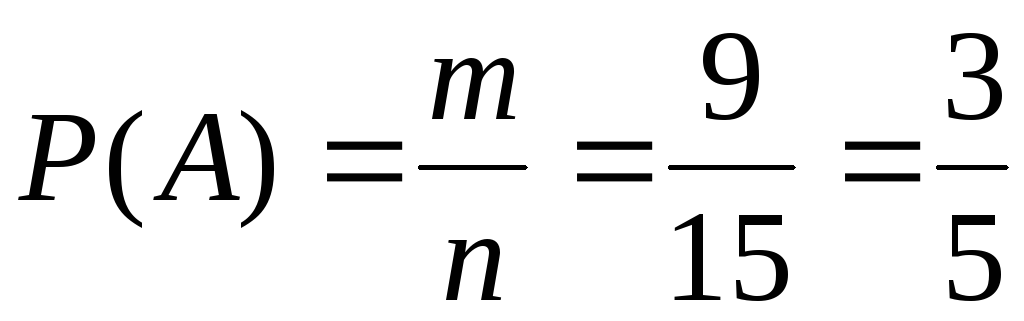Операції над подіями

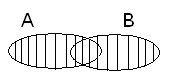
Додавання. Сумою двох подій А і В називається така подія С=АВ (С=А + В), яка внаслідок експерименту настає з настаннямхоча б однієї з подій А або В. Подію АВ схематично зображено на рис. 1 заштрихованою областю.
Рис. 1 Операція об 'єднання подій А і В.
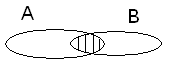
Множення. Добутком двох подій А і В називається така подія С = АВ (С = АВ), яка внаслідок експерименту настає з одночасним настанням подій А і В.
Операція АВ називається перерізом цих подій (рис. 2).
Рис. 2. Переріз подій А і В.
Приклад. Перерізом подій А = {2, 4, 6, 8, 10, 12} і В = {3, 6, 9, 12} є подія С1 = {6}, а сумою є подія С2 = {2, 3, 4, 6, 8, 9, 10, 12}.
Якщо 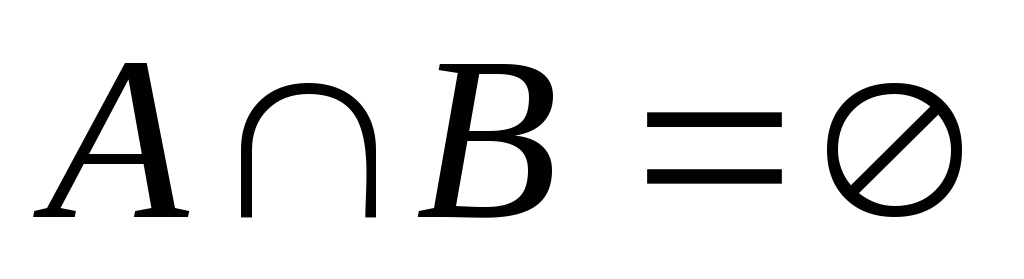, то випадкові події А і В називають несумісними. Якщо , то такі випадкові події А і В називають сумісними.
Повна група подій. Якщо 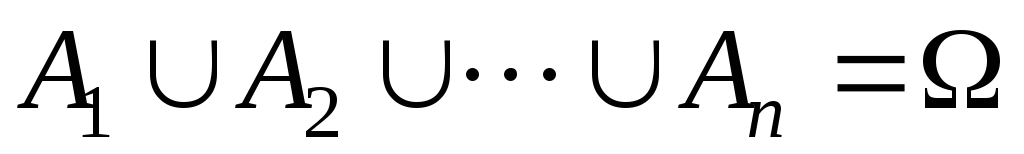, то такі випадкові події утворюють повну групу, а саме: внаслідок експерименту якась із подій {Аi} обов'язково настане.
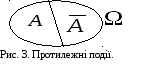
Протилежні події. Дві несумісні випадкові події, що утворюють повну групу, називають протилежними.
Подія, яка протилежна А, позначається . Протилежні події у просторі елементарних подій ілюструє рис. 3.
Елементарні випадкові події задовольняють такі твердження: 1) між собою несумісні; 2) утворюють повну групу; 3) є рівноможливими, а саме: усі елементарні події мають однакові можливості відбутися внаслідок проведення одного експерименту.

Питання для самоконтролю

  1. Що називається вірогідною; неможливою подією? Навести приклади.
  2. Яка подія називається випадковою? Навести приклади.
  3. Яка подія називається елементарною; складеною випадковою подією? Навести приклади.
  4. Що називається простором елементарних подій? Навести приклади.
  5. Що називається сумою, добутком, різницею двох випадкових подій А і В?