Використання формул комбінаторики для обчислення ймовірностей подій
АЛГЕБРА
Тема 3: Початки теорії ймовірностей Використання формул комбінаторики для обчислення ймовірностей подій
https://www.youtube.com/watch?v=OnfgaHQUVLEЕлементи комбінаторики
Щоб обчислити ймовірність тієї чи іншої випадкової події для певного класу задач із дискретним і обмеженим простором елементарних подій, необхідно вміти обчислити кількість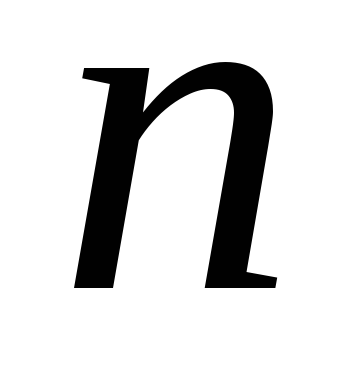 
усіх елементарних подій (елементів множини
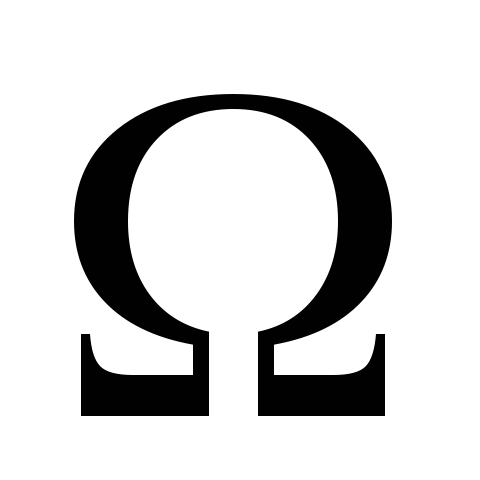) і число
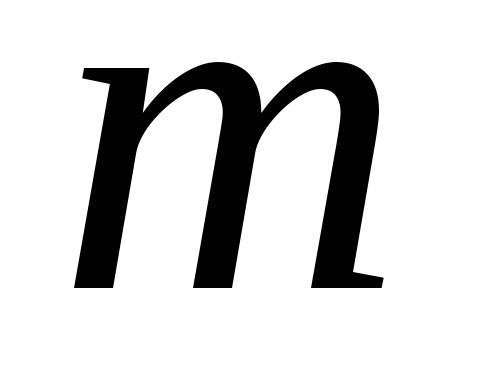елементарних подій, які сприяють появі випадкової події.
усіх елементарних подій (елементів множини) і числоелементарних подій, які сприяють появі випадкової події.
Існує клас задач, в яких для обчислення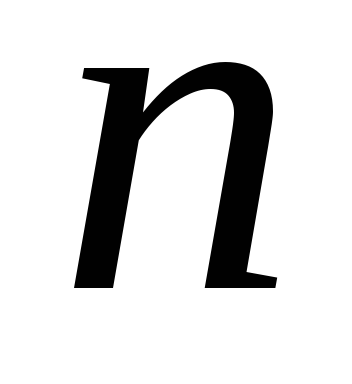 
і
використовуються елементи комбінаторики: переставлення, розміщення та комбінації. У комбінаториці оперують множинами однотипних елементів.
і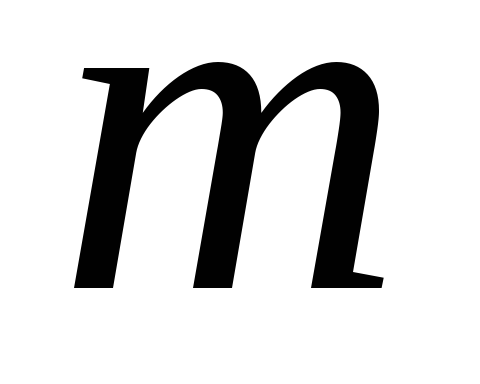використовуються елементи комбінаторики: переставлення, розміщення та комбінації. У комбінаториці оперують множинами однотипних елементів.
Загалом множини бувають упорядковані та невпорядковані.
Множину називають упорядкованою, якщо при її побудові істотним є порядок розміщення елементів. У противному разі множину називають невпорядкованою.
Перестановки. Перестановками із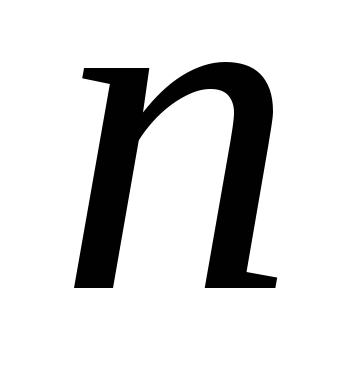 
елементів називають такі впорядковані множини з
елементів, які різняться між собою порядком їх розміщення.
елементів називають такі впорядковані множини з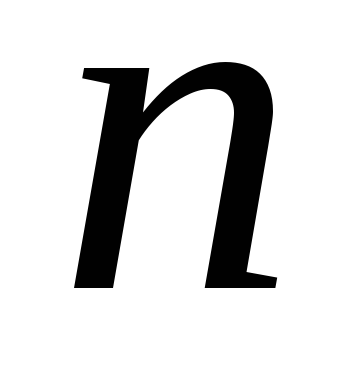елементів, які різняться між собою порядком їх розміщення.
Кількість таких упорядкованих множин обчислюється за формулою
, (2.2)
де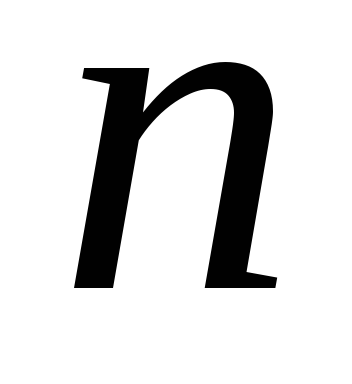 
набуває лише цілих невід'ємних значень.
набуває лише цілих невід'ємних значень.
Приклад 1. Задано множину цілих чисел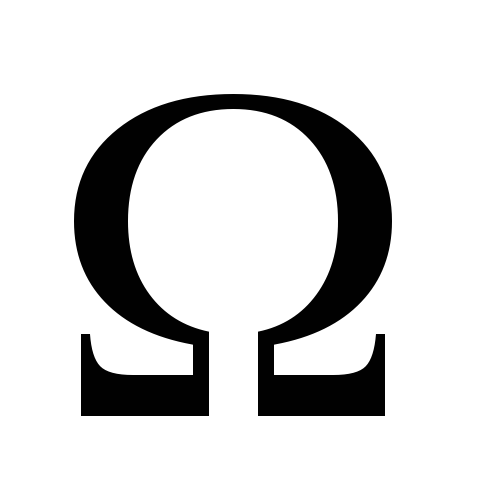 
= {1, 2, 3, 4, 5}. її елементи навмання розставляють у рядок. Обчислити ймовірності таких випадкових подій:
= {1, 2, 3, 4, 5}. її елементи навмання розставляють у рядок. Обчислити ймовірності таких випадкових подій:
А — розставлені в ряд числа утворюють зростаючу послідовність;
В — спадну послідовність;
С — цифра 1 стоятиме на першому місці, а 5 — на останньому;
Розв'язання.
Простір елементарних подій для цього експерименту міститиме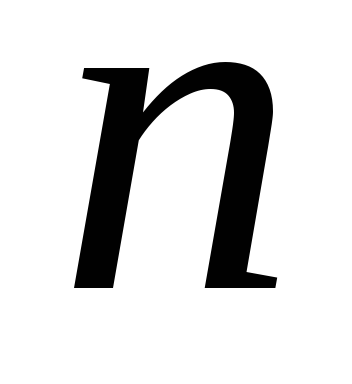 
=5!=1·2·3·4·5=120 несумісних, рівноможливих елементарних подій.
=5!=1·2·3·4·5=120 несумісних, рівноможливих елементарних подій.
Кількість елементарних подій, що сприяють появі А дорівнює одиниці (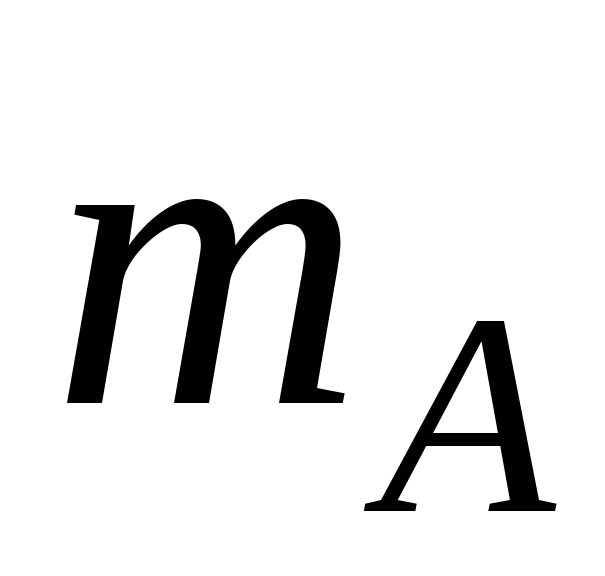
= 1). Кількість елементарних подій, що сприяють появі В дорівнює одиниці (
= 1). Для випадкової події С
= 3!. Тоді
= 1). Кількість елементарних подій, що сприяють появі В дорівнює одиниці (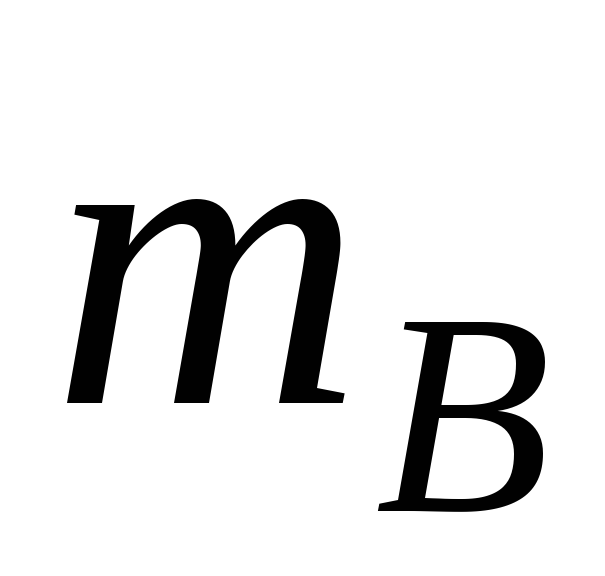= 1). Для випадкової події С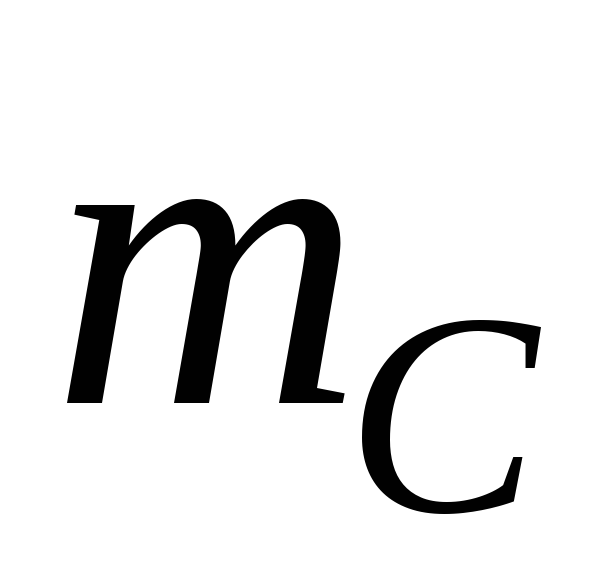= 3!. Тоді
, 
,
.
Розміщення. Розміщеннями із n елементів по m (0 < m < n) називаються такі впорядковані множини, кожна з яких містить m елементів і які відрізняються між собою порядком розташування цих елементів або хоча б одним елементом.
Кількість таких множин обчислюється за формулою
. (2.3)
Наприклад,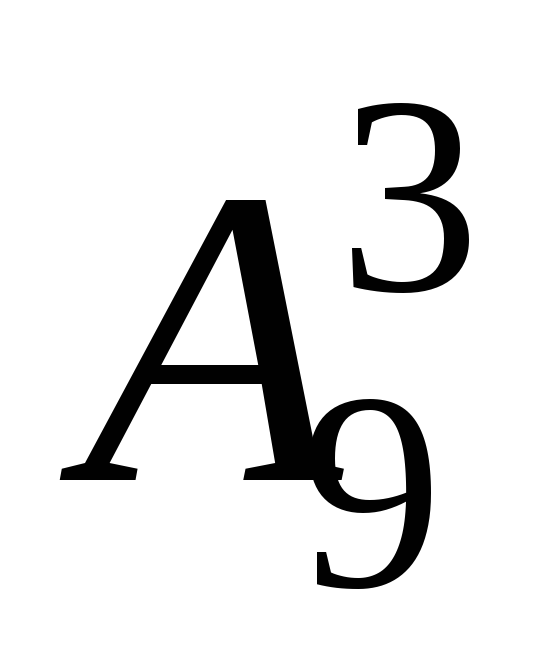 
= 9 ·8 ·7 = 504 .
= 9 ·8 ·7 = 504 .
Комбінації. Комбінаціями з n елементів по m (0 < m < n) називаються такі множини з m елементів, які різняться між собою хоча б одним елементом.
Кількість таких множин
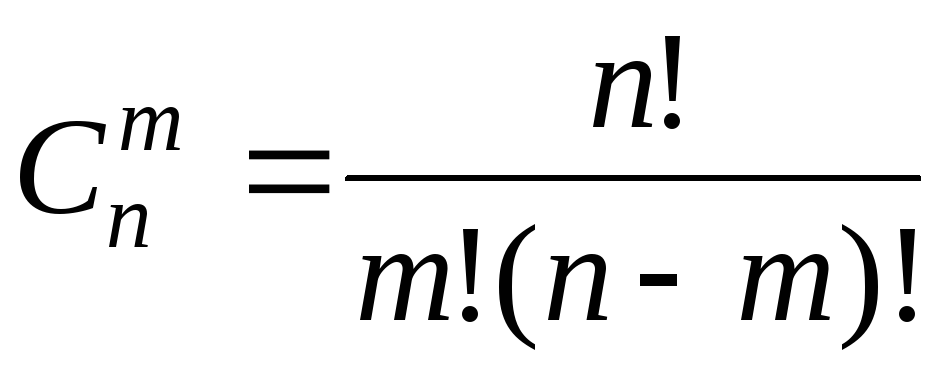. (2.4)